Tutorial : Geometric Patterns(2)
Following on from the previous tutorial where a simple square or rectangle was created from the Object coordinates, we can take this a step further by using a different coordinate system : polar (or cylindrical) coordinates - where each point in space is represented by a distance, and angle (and an elevation from the plane in the case of 3D cylindrical coordinates).

Point P is a specific point in XY space - where particular values of 'x' and 'y' can uniquely reference that point in space. However, sometimes it can be more convenient to measure the point using a difference coordinate system - in the case of Polar coordinates, the point is referenced based on an angle (theta) and distance (r) from the origin (where X and Y axes cross at zero). We can make use of the distance and angle to create difference patterns.
Polar Coordinates
In order to convert from X,Y,Z coordinates (known as 'Cartesian coordinates') into Polar coordinates we need to be able to calculate the distance from the origin (in the XY, YZ or XZ plane, depending on the orientation of the polar coordinates required) and the angle between some reference direction (usually one axis) and the direction to the point in space. For the distance, we can use Pythagoras Theorum as :
distance = sqrt(x*x + y*y)
For the angle we can use the 'atan2' function as :
angle = atan2(y,x)
Using Node Expressions, we can express this as follows :
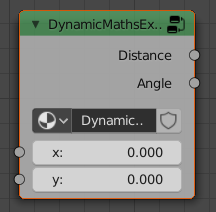
Distance = (x*x + y*y) ** 0.5, Angle = atan2(y,x)
This will produce a group node as follows :
Alternatively, if you'd prefer to use a Vector as input then you can use alter the expression to use vector notation as follows :
Distance = (Input[x]*Input[x] + Input[y]*Input[y]) ** 0.5, Angle = atan2(Input[y], Input[x])
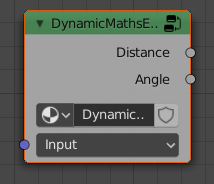
In this form, the Angle output will be in Radians - where there are 2xPi radians (approximately 6.28) in a whole rotation, ranging from -3.1415 to +3.1415 (ie, negative Pi to positive Pi).
For convenience we can adjust the calculate to produce an Angle value to represent the rotation from a range of 0.0 to 1.0 by including additional maths to divide by 2*Pi and offset by half a rotation :
Distance = (Input[x]*Input[x] + Input[y]*Input[y]) ** 0.5, Angle = atan2(Input[y], Input[x])/2/3.1415 + 0.5
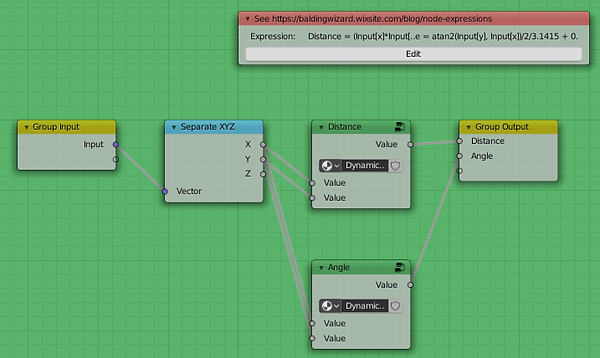
The generated group consisting of two sub-groups - one for Distance and the other for Angle.

The generated sub-group for the Distance calculation - essentially "sqrt(x*x+y*y)".
The generated sub-group for the Angle calculation - essentially "atan2(x/y)/(2*Pi) + 0.5" - however, note that 'atan2' has been expanded to use nodes which are compatible with earlier versions of Blender (at 2.79b, for example, 'atan2' is not a valid Maths function). A later version of the add-on will use the 'atan2' function for improved efficiency (but such node groups would not be able to be imported into an earlier version of Blender).
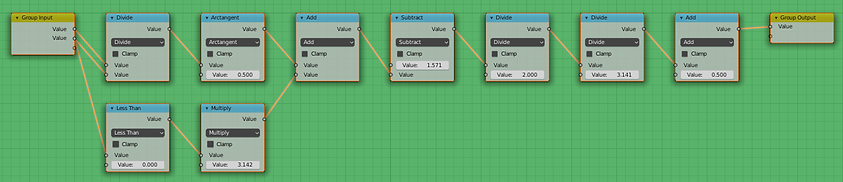
Of course, if you're not using Node Expressions you can manually create the nodes to perform the same calcultion instead.
Circle
Once we have Polar coordinates it opens up many possibilities. For example, to create a Circle we simply need to use the Distance from the origin - since all points within a circle are within the 'radius' of that circle :
Output = Distance < Radius

Adding some variation (using a Wave texture or Sine function) based on the distance produces concentric circles :

Spiral
Changing the output based on both the distance and the angle can produce spiral effects :

Star
The angle of rotation can be used to vary the distance in various different ways. By using a repeating function (such as Sine or Cosine) star-like patterns can be produced.
For example, using the following expression will produce an output based on the distance varied via a Sine wave to produce a star :
Output = Distance - 0.1 > (sin(Angle*5)+1)/15+0.2

